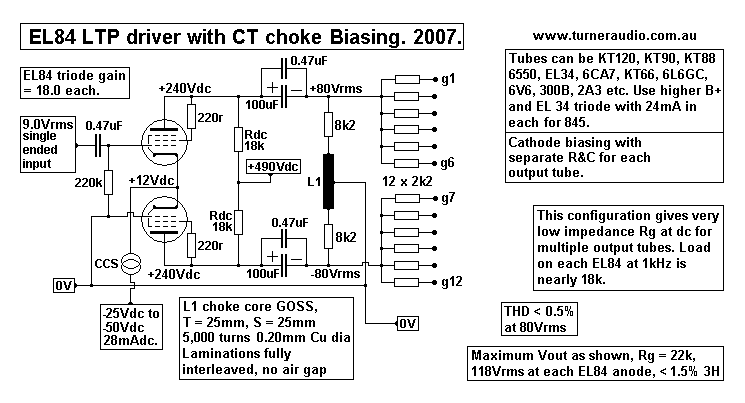
| 1 |
2 |
3 |
4 |
5 |
6 |
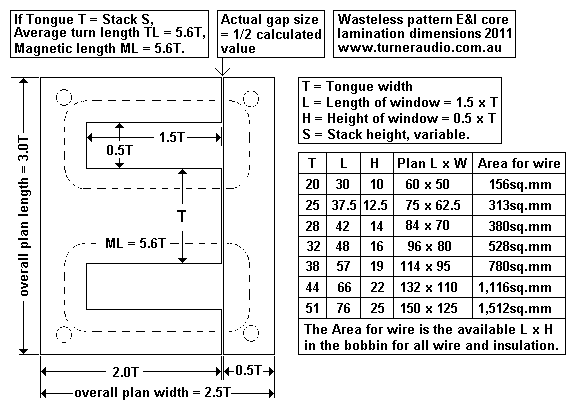
| Wasteless
E&I Square Afe, T mm x S mm |
Core
window e L mm x H mm |
Bobbin
winding area L mm x H mm |
Turns
0.15mm Cu dia, oad 0.188mm L in Henry µe = 2,000 |
Turns
0.20mm Cu dia, oad 0.245mm L in Henry µe = 2,000 |
Turns
0.25mm Cu dia, oad 0.301mm L in Henry µe = 2,000 |
| 25mm
x 25mm |
37.5
x 12.5 |
33
x 9.5 = 313sq.mm |
8,000t
720H |
5,000t 281H |
3,000t 101H |
| 28mm
x 28mm |
42
x 14 |
38
x 10 = 380sq.mm |
10,000t 1,260H |
6,000t 453H |
4,000t 201H |
| 32mm
x 32mm |
48
x 16 |
44
x 12 = 528sq.mm |
14,000t 2,822H |
8,000t 921H |
5,200t 389H |
| 38mm
x 38mm |
57
x 19 |
52
x 15 = 780sq.mm |
20,000 6,840H |
11,500t 2,261H |
8,000t 1,094H |